|
天空率計算の考え方 |
i-ARMにおける天空率計算の考え方の説明です。
天空率の計算は「天空図の作成」とその図を利用した「天空率の算定」の二つの段階に分けられま
す。また確認申請時に、検証用として三斜求積による天空率の算定を要求されます。
| 天空図の作成 | 天空図に基づく天空率の計算方法 | i-ARMでの天空率計算方法 |
※以下、太字の大文字はベクトルを示します。
i-ARMでは天空図を作成する場合、図1のように+Y軸方向を真北とした座標系を定めます(Z軸は紙面に垂直な方向です)。

図1の点Pを天空図を作成する算定点とし、点Tを天空図上に投影する計算点(建物の頂点など)とします。
図2は点Pを中心とした半径Rの天球です。
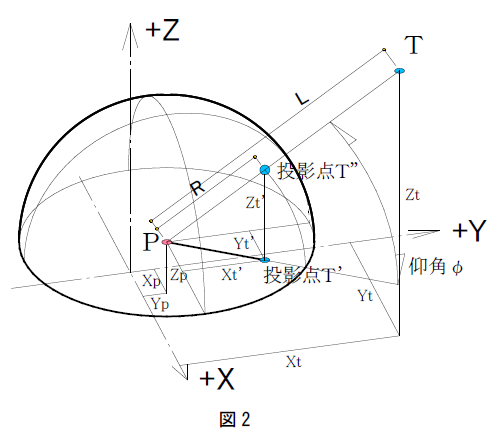
図2の天球上のどこに点Tが投影されるかを計算するための式が以下の式です(投影された点を投影点T”とします)。
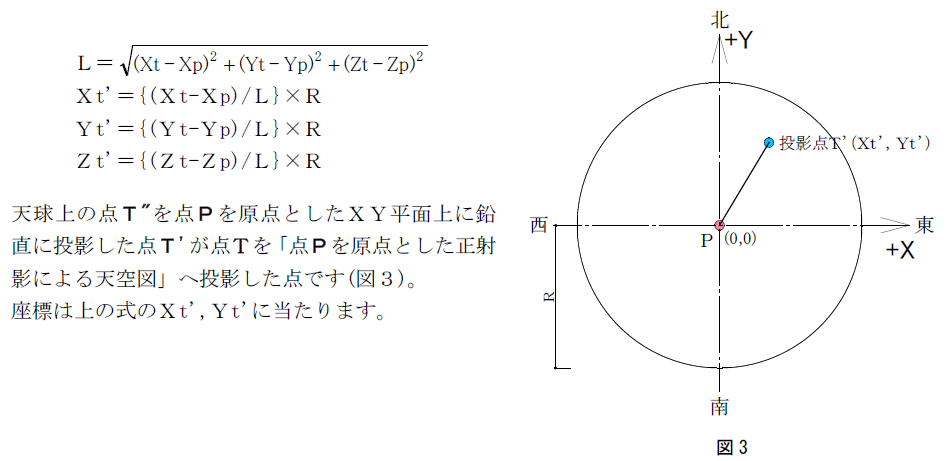
方位角θ、仰角φは次の式で算出できます。
方位角θ(+Y方向(北)を0度として西回りを+、東回りを-とする)
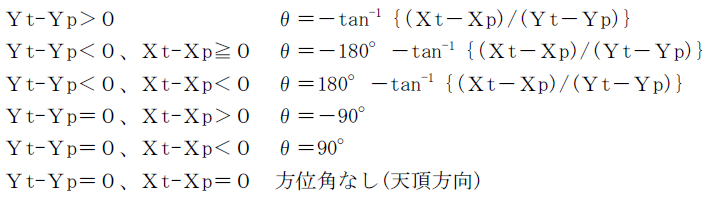
仰角φ(水平方向を0°、天頂を90°とする)
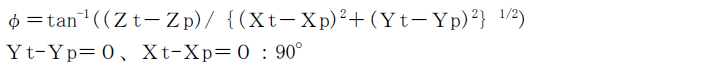
天空図の曲線部分の作図座標系内の線分(建物の稜線など)を天球上に投影するとすべて大円(弧)になります。大円(弧)をXY平面に投影すると楕円(弧)になります。 i-ARM は基本的に線分しか取り扱いませんので、天球面上で大円(弧)を多角形で近似してからXY平面に投影します。多角形は偏差が半径の1,000 分の1以下になるように設定しています。 大円: 球面上に描かれる円の内、その中心が球の中心と一致する物をいいます。半径が球の半径に等しくなります。 偏差: 円を多角形で近似する場合の、多角形の各辺と辺に対応する弧との隙間の間隔。偏差が小さいほど多角形の角数が多くなり、円と多角形の差が小さくなります。
|
i-ARMでは天空率の計算方法として、メッシュ法と算定求積法を採用しています。
i-ARMにおける、メッシュ法の計算方法の説明です。
コンピュータ内部で天空図を描き、建物が投影されていない時の天空図の円内に描かれたドットの数と、建物を投影したあと建物以外の空の部分のドットの数を数えて比較し、天空率を計算します。
例
算定点Aにおける、メッシュ法での天空率を計算してみます。
算定点Aでの天空図では、建物頂部の1~4の点がそれぞれ1'~4'に投影されています。
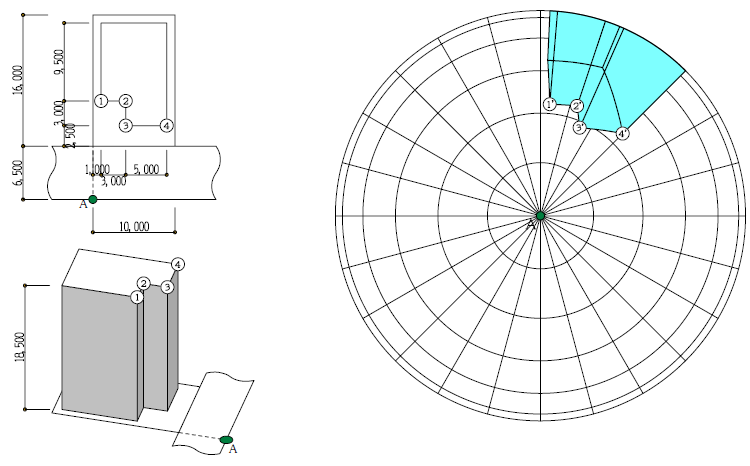
図4
天空率(U)は天空図全体の面積(S)と建物の投影図が占めている面積(B)が判れば、U=(S-A)/Sで求めることができます。
天空図をコンピュータのグラフィックメモリ上に作図します。
グラフィックメモリは図5のように格子状に配置されたピクセルの集まりですから、ピクセルの数を比較することで天空率を求めることができます。
まず、天空図を示す円だけを白で塗り潰して作図します。この例では26×26=676ピクセルのうち白く塗り潰されたピクセルの数は448個です。これがAに当たります。
次に建物の投影された部分(範囲)を黒く塗り潰します。すると、白く塗り潰されたピクセルの数は406個になります。これがS-Aに当たります。天空率Uは406/448=0.906で90.6%になります。
i-ARMでは3584×3584ピクセルの大きさで計算しています。
これはSに数えられるピクセルの数が1000万個以上になるように縦横のピクセル数を決めたためです。これにより計算単位は0.00001%になります。
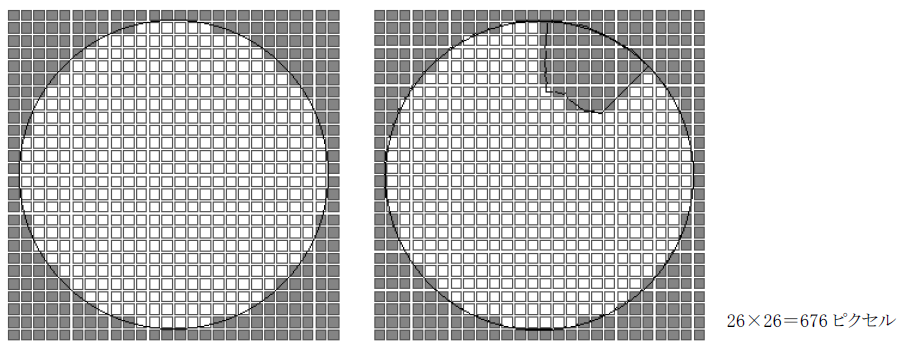
図5
i-ARMにおける、算定求積法の計算方法の説明です。
円の中心から建物の屋根の稜線(楕円弧)を直線で分割し、多角形にして面積を計算します。三角形の分割角度を細かくする事で楕円弧に近似します。
安全側に評価するため、適合建物を外接の多角形近似、計画建物を内接の多角形近似として計算します。
適合建物:外接近似
天空率を大きめに評価する→建物が小さくなるようにする→外接近似
計画建物:内接近似
天空率を小さめに評価する→建物が大きくなるようにする→内接近似
例
半径1(単位円)の天空図で考えます。
建物上の点A1、点B1は、XY平面(天空図の作図面)上の点A、点Bに投影されます。
点A、点Bは天球面上の点A'、点B'をXY平面に正投影したものですから、
A'(Ax,Ay,Az)=A1/|A1|およびB'(Bx,By,Bz)=B1/|B1|となり、
これより点A、点BはA(Ax,Ay,0)およびB(Bx,By,0)となります。
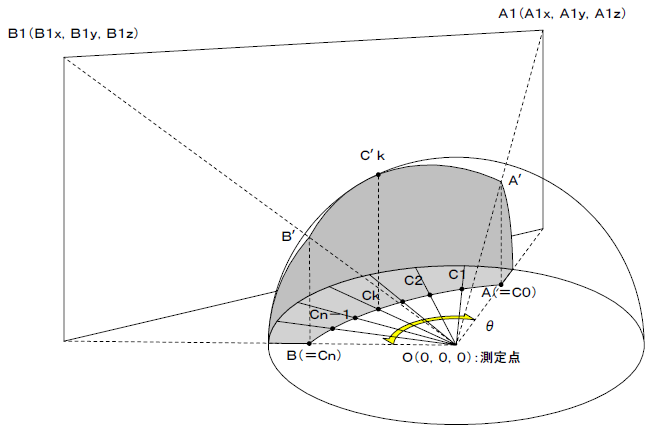
図6
この建物の投影面積Sを三斜求積で求めます。
扇型OABの頂角をθとすると、
θ=arccos((A・B)/(|A|×|B|))[arccos:逆余弦]
三斜求積のための分割角度の基準値を10度とすると扇型OABはn個の三角形に分割されます(n:θ/10より大きな最小の整数)。
三角形はそれぞれ、△OC0C1,△OC1C2,・・・△OCn-2Cn-1,△OCn-1Cnと表わされます。
C0=A、Cn=B
楕円弧上の点Ck(k=1~n-1)を求めます。
Ckは天球面上の点C'kの正投影ですから、まずC'kを求めます。
XY平面に含まれたOCkに直行する単位ベクトルCkは、
Ck((Ax×cosφ-Ay×sinφ)/|A|,(Ax×sinφ+Ay×cosφ)/|A|)となります(φ=k×θ/n+90°)。
C'k(Ckx,Cky,Ckz )=ck×(A'×B')/|ck×(A'×B')|だから、Ck(Ckx,Cky,0)となります。
△OCk-1Ckについて(k=1~n)
底辺 Wk=|Ck-1|
高さ Hk=|Ck-1×Ck|/|Ck-1|
面積 Sk=Wk×Hk/2
天空図の外周と頂角θでできる扇型の面積SO=π×(θ/360°)なので
建物の投影面積はS=S-ΣCkとなります。
i-ARMでの計算方法は以下の通りです。
天空率一覧表
 天空率計算はすべて三斜求積法で求める:三斜求積法
天空率計算はすべて三斜求積法で求める:三斜求積法
 天空率計算はすべて三斜求積法で求める:メッシュ法
天空率計算はすべて三斜求積法で求める:メッシュ法
三斜求積図
三斜求積法
補足1:
“□天空率計算はすべて三斜求積法で求める”(OFF)の場合は、天空率一覧表をメッシュ法で行い、三斜求積図を三斜求積法で求めます。
そのため、同じ算定点の天空率を計算しても、値が一致しない事が多くなります。
計算方法が異なるため、値が一致しないことは問題ありません。
補足2:
斜線制限の天空率代替における天空率計算の計算方法には指定がありません。
「確実に安全側で計算できる三斜求積で計算を行い、結果を比較して適合/不適合について同じ結果が出ていれば問題ないとする」となっています。
つまり、「適切に行われた三斜求積による計算の方が確実に安全側で計算できる」という前提があります。
適切に作図された三斜求積天空率は必ず、内接による三斜求積天空率≦真の天空率≦外接による三斜求積天空率となり、しかも計算過程を手作業で確認できます。
一方、一般のソフトウェアによる計算結果はその計算方法が特定できない限り、結果を検証することはできません。また、計算方法が特定できても手計算で検証できない可能性があります。
そのため、計画建物の天空率と適合建物の天空率の値が接近している場合、手計算で検証するために三斜求積図とそれによって計算した天空率の提出が求められます。
そのため i-ARMでは、天空率一覧表においても、確実で安全側で計算できる三斜求積法で求める設定があります。(□天空率計算はすべて三斜求積法で求める)
