i-ARMにおける日影計算の考え方の説明です。

※以下、太字の大文字はベクトルを示します。

◆太陽の位置

日影に関する様々な計算の基礎となるのは、任意時刻の太陽の位置です。それは、以下のような式で計算します。

ここでは太陽の位置を、天頂をＺ軸の＋方向、真北をＹ軸の＋方向とした座標系における単位方向ベクトルＳ(Ｓx、Ｓy、Ｓz)で表しています。

Ｓx＝－cos(δ)・sin(τ)

Ｓy＝sin(δ)・cos(φ)－cos(δ)・cos(τ)・sin(φ)

Ｓz＝sin(δ)・sin(φ)＋cos(δ)・cos(τ)・cos(φ)

ここに、

δ：赤緯（－23.4°(冬至)～＋23.4°(夏至))

φ：緯度（－90.0°(南極点)～＋90.0°(北極点))

τ：時角（－180.0°(午前０時)～＋180.0(午後12時)）

また、

τ＝(Ｔ－12)・15

Ｔ＝ｔ＋(Ｌ－135)/15＋ｅ

Ｔ：真太陽時(測定点において太陽が南中した時刻を12時とします。)

ｔ：中央標準時(国や地域が共通で使う時刻系です。日本では、東経135°(兵庫県明石市)において太陽が南中した時刻を正午とします。)

Ｌ：東経(日本国内(122°55′59″(日本の西端)～153°59′12″(日本の東端))またはＵＴＣ(協定世界時）＋９の地域)

ｅ：均時差(標準時では、一日の長さは年間を通して同じですが、地球の軌道が楕円であることと地軸が公転軌道面に対して傾斜しているため、実際には一日の長さは変化します。均時差はその実際の一日と標準時上の一日の長さのずれを示します)

なお、上記のＸ、Ｙ、Ｚを使うと、日影規制で使われる係数は、

方位角        Ａ＝tan-1(Ｓy／Ｓx)

倍率                Ｍ＝(Ｓx2＋Ｓy２)1/2／Ｓz

高度(仰角)        Ｉ＝tan-1(Ｓz／(Ｓx2＋Ｓy2)1/2）

で、算出できます。

◆時刻日影

時刻日影図

受影面の高さをＺ＝ｈとすると、

建物の任意の位置Ｐ(Ｐx、Ｐy、Ｐz)の受影面上での位置Ｑは前項の太陽の方向を示す単位ベクトルＳを使い、

Ｑ＝Ｐ－Ｓ ・｛（Ｐz－ｈ) / Ｓz ｝

となります。

このＱを建物の各頂点について計算し、それをつないだ物が(太陽の方向がＳである場合)時刻日影図となります。

日影チャート(任意の点の日影時間)

i-ARMでは、任意の点の日影時間の計算に連続法を使っています。

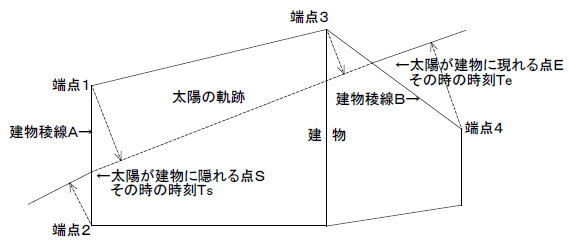
これは太陽の軌跡と建物の位置関係を図形方程式化し、太陽が建物に隠れる時刻、太陽が建物から現れる時刻を方程式の解から求め集計することにより、日影時間を求める方法です。

以下のような手順で計算します。

１．太陽軌道と建物稜線の位置関係を表す関数Ｆ(Ｐ)を導きます。太陽の軌跡の方が上にあるときは関数値が正、下にあるときは関数値が負となるように設定します。

２．各稜線について１．を求め、以下の関係のある稜線を選びます。

端点１(１x、１y、１z)における関数値Ｆ(端点１)＜０

端点２(２x、２y、２z)における関数値Ｆ(端点２)＞０

区間(端点１、端点２)でＦ(Ｓ)＝０(Ｓ：太陽が建物に隠れる点)と､その時の時刻Ｔsを求めます。

３．同様に、

端点３(３x、３y、３z)における関数値Ｆ(端点３)＜０

端点４(４x、４y、４z)における関数値Ｆ(端点４)＞０

なる稜線を特定します。Ｆ(Ｇ)＝０(Ｇ：太陽が建物から現れる点)と､その時の時刻Ｔｇを求めます。

４．すべての建物についてＴsとＴｇを求め、その和集合(∪)をとるとそれが日影時間となります。

◆等時間日影線

追跡法

i-ARMでは、等時間日影図の作成に追跡法を使っています。

等時間線上の点の接線方向付近を検索、追跡するようにして、等時間線を描く方法です。最初の点は建物稜線付近をチェックし、受影面上の日影時間を一定間隔で求める(メッシュ法)などの方法で求めます。等時間線付近を集中的にチェックするため、一般に高速で作図できます。

等時間日影計算における誤差

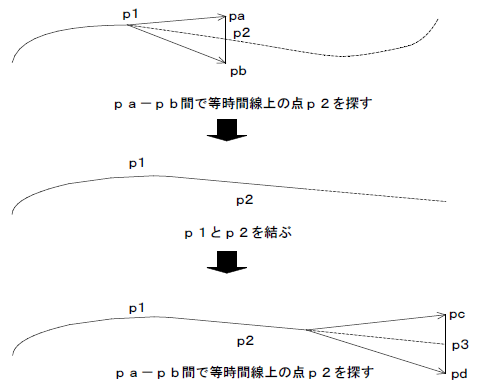
等時間日影計算では、必ずある程度の誤差が含まれます。

仮にＡ時間の等時間線を求める場合でしたら、i-ARMではメッシュ法で日影時間がＡ時間となる点を求め、その点を基準点とし周囲の日影時間を計算し、日影時間がＡ時間になる点を次の点として、基準点と繋ぐことを繰り返して等時間線を求めていきます(上図参照)。

このように、実際には建物の形状や基準点の建物に対する方向から、ある程度どっちに等時間線が進むかは推測できますのでその方向を中心に調べます。

この時、日影時間がＡ時間であると判断する精度が1.5秒～10秒前後になります。

次の点までの距離は建物形状や規模で初期値を決めますが、その位置にＡ時間になる点がない場合、次の点までの距離を最小２cm前後まで短くしていきます。

ただし、次の点までの距離が２cm前後になれば、前述した精度に係らず、５時間に最も近い点を次の点と見なします。

日影時間が２cm以下の距離で大きく変化する場合は、誤差はそれに追随することになります。

こうした僅かな距離の違いで日影時間が大きく変化する現象は、建物の北側でよく発生します。特に下図のように建物が東西に伸びており、屋根部分に凹凸がある場合に顕著です。

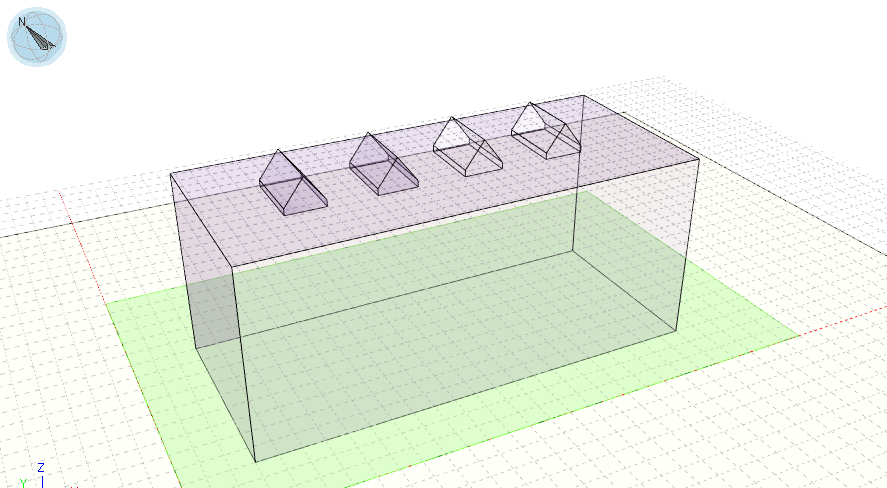
建物の北側では建物の屋根越しに12時前後の日が当たります。

12時前後は短くなってきた影が長くなりだす時刻で、その付近は、短い時間間隔で影になったり日が当たったりを繰り返しますので、狭い範囲で日影時間は細かく変化し、その付近における等時間線の誤差は大きくなります。

例では、１cm間隔で36点の日影時間を計算していますが、隣り合った(１cmしか違わない)点の日影時間が90秒近く変化している場所があり、前述の次の点までの距離が仮に最小の２cmになったとしても、1～2分近くずれる可能性があることになります。

１cmというと、これは1/100の図面上で0.1mmになり、仮に0.3mmの線幅で作図するとほぼ重なっていることになり、クリアしているかどうかの判定は、誤差を考慮する必要があります。

基本的には等時間線と測定線の間隔が２cm以下の場合は測定線上の日影時間を確認してください。

また今回の例のように東西に伸びた建物の12時前後の影が落ちる部分は、狭い範囲で日影時間が変化しますので、等時間線と測定線の間隔が２cm以上でも、最も等時間線と近い測定線上の点については、日影時間の確認をした方が安全です(「日影チャート(任意の点の日影時間)｣を参照)。

(建築基準法施行令規則第一条の三で指定されている表三(三十)の「日影図」で「測定線上の主要な点の日影時間」を図示することが求められていますが、多くの審査機関が上記のように等時間線が測定線に接近している点を「主要な点」として指定しています。

◆隣地の地盤面の高さが異なる場合の考え方

日影規制では、計画敷地が隣地より1m以上低い場合に、計画建築物が隣地に及ぼす日影の影響が少なくなるため、日影計算時に用いる地盤面の算定で緩和を受けられます。以下に例を示します。

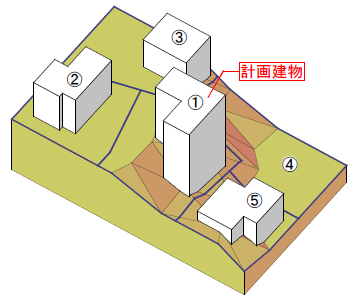
１．下図のように、傾斜地が５つの敷地に分かれているとする。①の敷地に建築物を計画する。

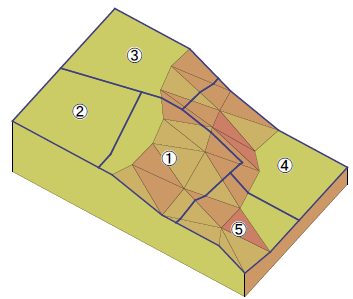
２．隣接する敷地の建物および①の敷地に計画した建物は下図のとおり。

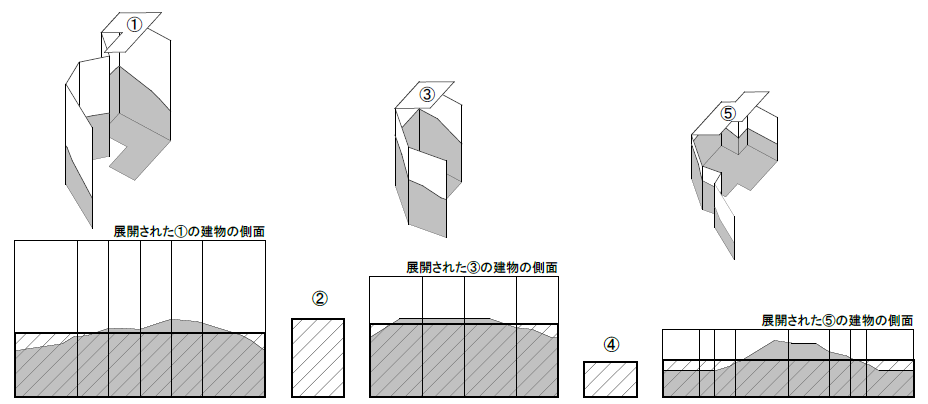
３. 建物と地面が接する部分の高さの平均が、敷地の平均地盤面となる(①､③､⑤)。

建物が地面と単一の水平面で接している場合、その水平面の高さが平均地盤面となる(②)。

建物がない場合、敷地内の土量を敷地面積で除した値が平均地盤面（平均地表面）となる(④)。

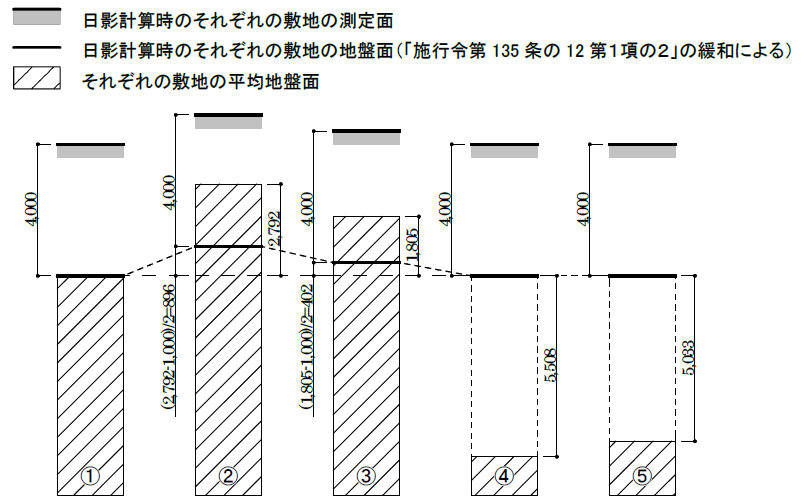
４. ①の敷地の平均地盤面の高さを基準にして、基準法上の緩和を考慮した日影計算時のそれぞれの地盤面の高さは以下のようになる。

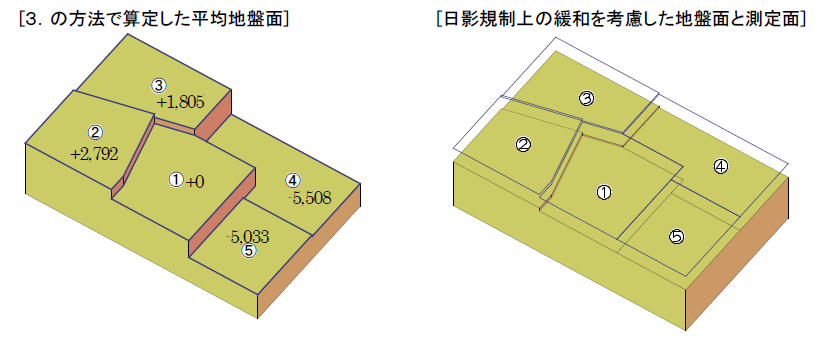
i-ARMでは、以下のように平均地盤面や地盤面を入力します。

日影計算時に用いられるそれぞれの地盤面高さの考え方